© 2021 次世代監査法人IPOフォーラム
All Rights Reserved.

上場準備会社において、ストックオプションは従業員へのインセンティブ報酬として欠かせない役割を担っています。近年では上場準備会社がストックオプションを利用しやすくなる税制改正も進み、ストックオプションの設計および価格算定の重要性が、より高まっていると感じます。
この記事はストックオプションの価格算定に焦点を当てています。発行会社や監査法人の担当者が外部専門家の評価をレビューする際に、中身を吟味できるよう、価格算定方法の理解促進を目的としたものです。
ストックオプションの評価方法は大きく分けて3つあります。ブラック・ショールズのオプション価格式、モンテカルロ法および二項モデルです。
名前を知っている方や、おおまかなイメージを持っていらっしゃる方もいらっしゃるでしょう。しかし、これらの計算実務では、専用の有料ソフトを使うことが多く、実際に手を使って計算されたことがある方は少ないのではないでしょうか。
この記事で、みなさんにExcelでシンプルなストックオプションの評価(ブラックショールズとモンテカルロ法)を疑似再現してもらい、難解なイメージをもつオプション評価を手触り感のあるものにしていただければと思います。 マクロも使いませんので、気楽にお試しください。
まず、ストックオプションの評価に用いる基礎的な6つの前提について紹介します。
Excelモデルを作る際、この6つの前提が変動したときにどのようにオプション評価に影響を与えるのか理解しておくと、より評価方法の理解が進むと思います。
Excelの計算のみを試されたい方は、次の章に進むことをお勧めします。
オプション設計をする際に自由に設定できるもの(下記の(1)と(2))と、市場の情報等から理論上一意的に定まるもの(下記の(3)~(6))があります。
後者について、その前提の変化がオプション価値に与える感度を議論することの実務上の意義はそこまで高くないのですが、3章以降でシミュレーションするために、理解しておくと役立つと思います。
以降の説明は、権利行使タイミングが満期時に1回のみのヨーロピアンタイプのコールオプションを想定しています。また、理解目的を優先して、理論上の説明を簡略化しているため、留意してください。
オプションを行使して株式を手に入れる際に、あらかじめ定められた金額を支払う必要があります。その金額がオプションの行使価格です。
100円払って株式を手に入れることができる権利と、150円払って同じ株式を手に入れる権利を比較した場合、100円で手に入れる方が、うれしいと思います。その分、オプションの価値は高くなります。
オプションの行使価格が安いほど、オプションの価値は高くなります。
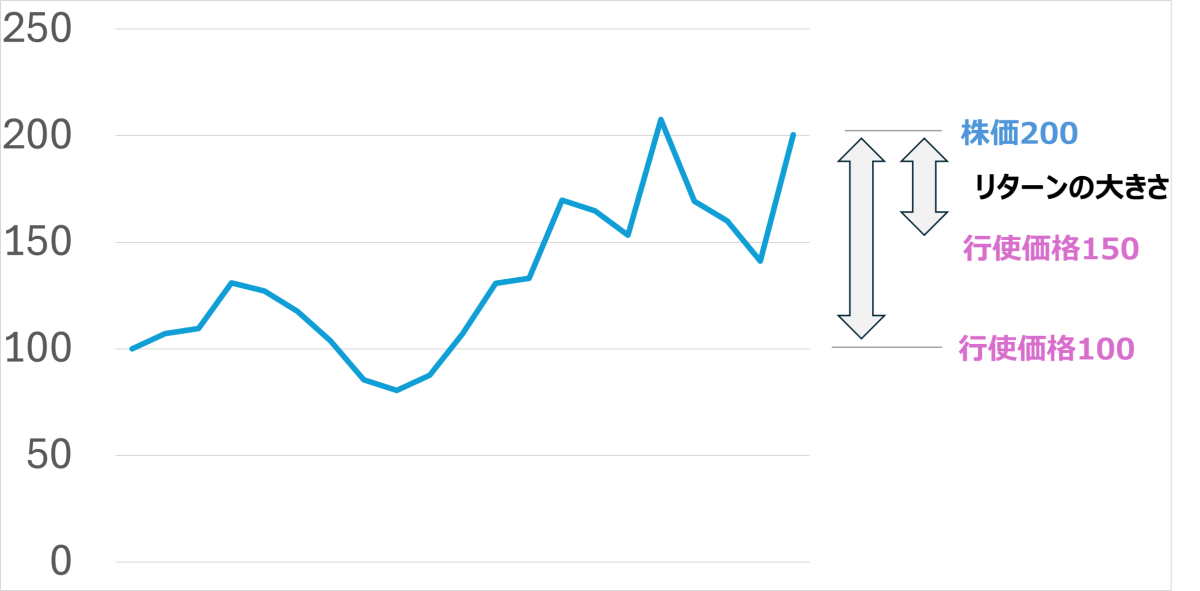
オプションを持っている人が、権利を行使すると想定される時点までの期間です。オプション価値に与える影響は、権利行使して手に入る株価との関連性で考えると、理解がしやすいと思います。
たとえば、1年間に株価が100円の幅で変動する初期株価100円の株を仮定します。1年後は1円~200円です。2年後には1円~300円の幅になります。期間が1年から2年に延びたことで、上限は200円から300円に増えており、株価が高くなる可能性が増えています。
同時に、株価が下がる可能性も増えていますが、行使価格より株価が下がったときは、オプションを行使しなければよく、上がる可能性のみに着目できるので、期間が長くなる方がオプションの価値は高くなります。
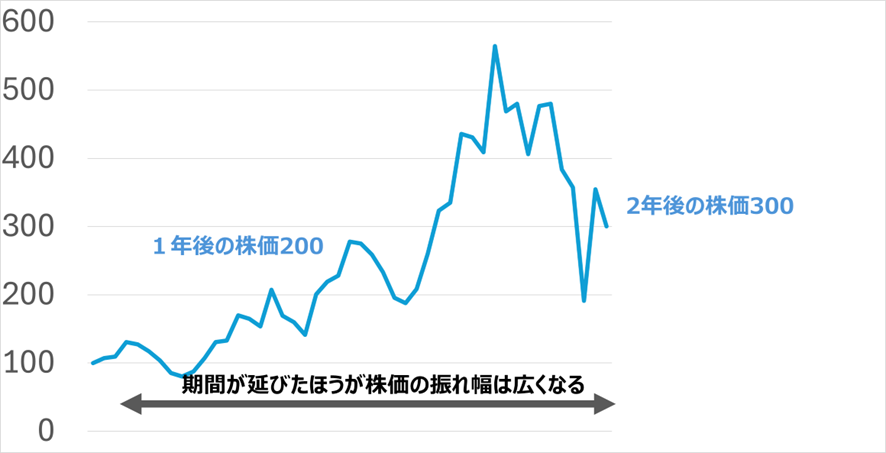
オプションの価値をシンプルに表すと、手に入れられる株価から、行使価格を差し引いたものになります。すなわち、行使価格対比で、株価が大きければ大きい方がオプションの価値が高くなります。
仮に、100円の行使価格で初期株価が100円の場合と、おなじ行使価格で初期株価200円だった場合、高い株価になるチャンスは当然200円の方が大きいため、(1)の理屈と同じですが、オプションの価値が高くなると考えます。

この前提は、株価の値動きがどれだけ激しいかを示すものです。過去の株価や、上場前の株であれば類似企業の過去の株価情報をもとに、値動きの激しさを計算します。ボラティリティ、ボラと言ったりします。
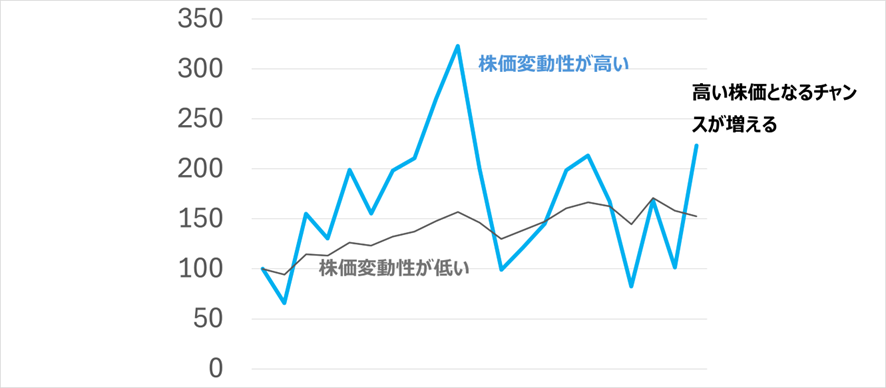
満期までの値動きの幅が、①±25円の株と、②±50円の株を比較します。②は値動きが激しいので、株価変動性が高いといいます。
今の株価を100円とすれば、満期時に①は75円~125円、②は50円~150円と予測されます。(2)と同様に、②のほうが上限が150円と①より高いので、得られるリターンの期待値もその分高くなります。
そのため、株価変動性は高い方がオプションの価値が高くなります。
この株価変動性は、未上場企業の場合類似企業の株価変動率を参照して算出することになります。
そのため、見積の要素が高く、様々な留意点が基準上で定められています。(ストック・オプション等に関する会計基準の適用指針10項~12項)。外部専門家の評価書を確認する際には、この基準に照らして検討するとよいでしょう。
付与対象となる株への配当を予測して算定します。配当を多く実施する株ほど、配当落ちによって将来の株の価値は目減りしていきます。逆に配当しない株は、配当落ちによる株価下落は考慮しなくて大丈夫になります。
得られる株価は高い方が良いため、配当額は小さい方がオプションの価値は高くなります。未上場の会社では配当をしないケースが多いと思うため、その場合は0で計算します。
無リスクの利子率(割引率)は、自然に金銭や株価の価値が右肩上がりにあがる比率とイメージするとよいでしょう。この比率が高い方が、将来株価が高くなるため、上述の(2)~(4)の理屈と同様でオプションの価値が高くなると理解するとよいでしょう。

これらをまとめると、以下のようになります。
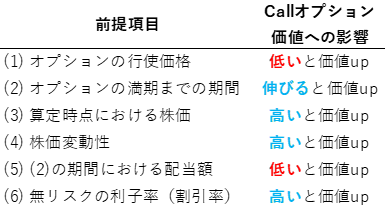
次の章では、実際にExcelにブラック・ショールズのオプション価格式を立式し、上記の想定通りの動きをするのか、試してみたいと思います。
ブラック・ショールズのオプション価格式は、満期時点のみで権利行使が可能なヨーロピアンタイプのオプションに用いられるものです。
2章で紹介した6つの前提数値が集められれば、即座に計算ができるため、使い勝手のよい式となっています。しかし、適用可能なオプションの種類は限定的で、最もシンプルなオプション(バニラオプション)にのみ使えます。権利行使条件が付されているなどの複雑なオプション評価には、そのままで用いることができません。その際は、次章で紹介するモンテカルロ法などを用いることになります。
オプション価格をcとすると、オプション価格は以下で示されます。
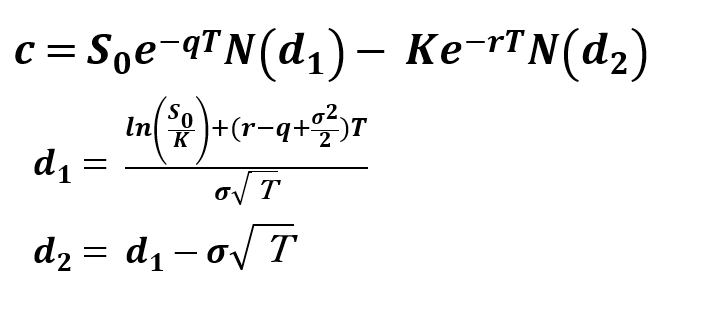
ここで、それぞれの文字記号と前章の前提の対応は以下になります。
K:オプションの行使価格(2章の前提(1))
T:オプションの満期までの期間(2)
S0:算定時点における株価(3)
σ:株価変動性(4)
q:配当率(5)
r:無リスク利子率(6)
すこし見慣れない文字記号もあると思いますので、簡単に補足いたします。
① e-():連続割引計算をしている数式です。 DCF法などで用いる割引計算、1/(1+r)2などを、連続時間に細分化したものです。たとえば、e―rtは、 t年後からr%で現在まで連続時間で割引計算をしているものとなります。eはネイピア数と呼ばれ、Excelでは、「=exp()」で計算します。
② N():標準正規分布の確率累積密度関数です。ざっくりと、確率というイメージを持つとよいでしょう。N(d)は、標準正規分布上の横軸-∞からdまでの区間の面積です。dが大きくなればなるほど、確率は高くなるとイメージすればよいです。Excelでは、「=norm.s.dist(,1)」で計算できます。
(Excelのバージョンによっては、上記の関数をサポートしていない場合があるため、そのときは、normsdist()をお試しください。)
③ Ln():自然対数です。Excel上では、「=ln()」で計算できます。
それでは、Excelでシミュレーションをしてみましょう。
ここでは、 K=100円、T=1年、S0=100円、σ=50%、q=0%、r=1%のオプションを想定したいと思います。以下がExcelに計算式を入れたものです。青字が計算式となります。
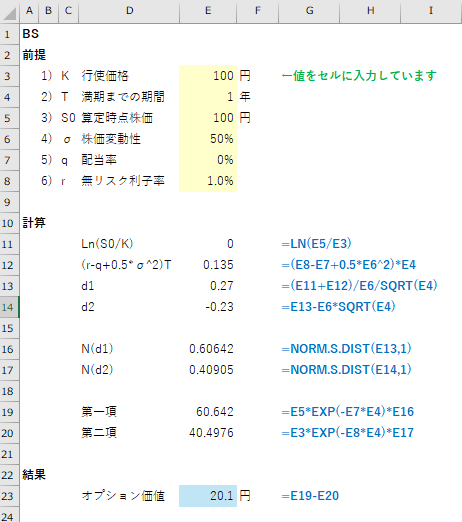
この通りに入力していただくと、計算結果がE23セルに表示されます。
試しに、各変数(E3セル~E8セル)を変動させてみてください。2章で記載した価格変動と同じ動きをすることが確認できると思います。
上記のExcelが見づらかった方のために、以下に計算式をテキストで記載していますので必要に応じて活用してください。
E11セル: =LN(E5/E3)
E12セル: =(E8-E7+0.5*E6^2)*E4
E13セル: =(E11+E12)/E6/SQRT(E4)
E14セル: =E13-E6*SQRT(E4)
E16セル: =NORM.S.DIST(E13,1)
上記がうまくいかない場合は =NORMSDIST(E13)
E17セル: =NORM.S.DIST(E14,1)
上記がうまくいかない場合は =NORMSDIST(E14)
E19セル: =E5*EXP(-E7*E4)*E16
E20セル: =E3*EXP(-E8*E4)*E17
E23セル: =E19-E20
それでは、次にモンテカルロシミュレーションをしてみましょう。
モンテカルロシミュレーションは、カジノで有名なモンテカルロ地方にちなんで名づけられたシミュレーション方法です。乱数等を用いたシミュレーションを複数回することで、将来予測を導き出すものです。
今回は、前章のブラック・ショールズの価格式で計算した条件と同じ条件で計算することで、その評価額が近似する様子をExcelで確認したいと思います。
将来の不確実な事項、今回の例でいえば、株価が将来どのように変動するかについて、乱数を用いてシミュレーションをします。用いるモデルは、株価が対数正規分布に従うとの仮定に基づいた以下の株価変動モデルを用います。

ブラック・ショールズの価格式の章で紹介した前提と同じものもありますが、新しい文字記号も2つ登場しています。はじめにこれらについて紹介します。
① Δt:シミュレーションのステップ幅です。権利行使の判断タイミングを想定して設定することが多いと思われます。たとえば、1週間に1度の権利行使の判断がおこなわれると想定した場合は、1÷52週≒0.02年が、Δtとなります。毎日行われるとした場合は、Δt=1÷250営業日=0.004年となります。
② ε:標準正規分布に従う確率変数です。これが乱数になります。シミュレーションを実施すると、このεは毎回異なる値を示します。
Excel上では、「=norm.s.inv(rand())」で計算できます。 (Excelのバージョンによっては、上記の関数ではうまくいかないため、その場合はnormsinv(rand())でお試しください。)
式の簡単な解説ですが、t時点における株価は、1時点前(t-1)の株価からrの無リスク利子率で成長し、qの配当率分だけ下落します。さらに、この変化に加えて株価変動要素σεがランダム項として、加味されていると理解するとよいでしょう。
Excelに落とし込むと、下記のようになります。

セルG24は、満期日に得られるキャッシュイン(ペイオフ)の計算をしています。株価が権利行使価格を下回ったときには、権利行使をしないので、ペイオフはマイナスにはならず、最低でも0になります。この状態を表現するために、max関数を用いています。ペイオフは将来に発生するので、ネイピア数eで現在価値に割り引いています。
これを1セットとして、複数セット実施します。Excel上では、コピーペーストで増やしていきましょう。

最後に、全セットのペイオフの平均値をとったものが計算結果です。(E11セル) コピペの数を増やせば増やすほど、ブラック・ショールズの価格式に近似していくのですが、漏れなくExcelの挙動も重くなっていくので、事前に作業中のファイルは保存しておくことをお勧めします。
画像が見にくかった方のために、計算式を以下に記しています。
D15~D24セル: =$E$10
E15~E24セル: =NORM.S.INV(RAND())
上記がうまくいかない場合は、=NORMSINV(RAND())
F14セル: =$E$5
F15セル: =F14*EXP(($E$8-$E$7-0.5*$E$6^2)*D15+$E$6*E15*SQRT(D15))
F16~F24セル: F15セルをコピーして貼り付けてください
G24セル: =EXP(-$E$8*$E$4)*MAX(F24-$E$3,0)
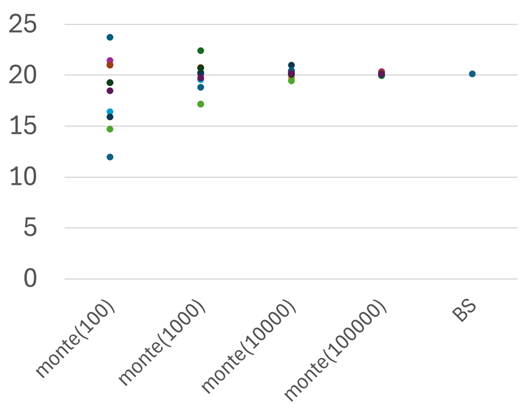
下記の図は、コピペの回数(モンテカルロ法の試行回数)を増やしていったときに、どのように値が収斂していくかをプロットしたものです。
一番右がブラック・ショールズ価格式で導き出した数字です。回数が少ないとばらつくのですが、回数を増やすにつれ、収斂していく様子が見て取れると思います。
以上では、シンプルなオプションを評価しました。
モンテカルロシミュレーションの利点は、さまざまな条件(株価がxx円のときには、オプションが失効する等)を設定できることです。
余力がある方は、以下の条件で試してみても良いでしょう。
| 上記のストックオプションにノックアウト条件が付与されたオプション。 ・期間中1度でも株価が初期価格の90%以下に下がった場合にオプションが消滅する ・ステップ幅は0.1年 |
うまく、条件式を組んで、コピペ回数を増やせば、14円程度の計算結果が出るので、お試しください。
最後になりますが、Excelスプレッドシート単体で実務に耐えられるシミュレーションをするには、乱数生成の厳密性や処理能力の制限などから、限界があります。今回ご紹介したExcelによる再現はあくまで学習用と割り切っていただけると幸いです。
参考文献)